Производительность
Продолжаем изучать элементарные задачи по математике. Сегодня мы рассмотрим очень интересную физическую величину — производительность.
Что такое сила?
Сила — это физическое явление, способное изменять форму материальных тел , вызывать их движение , менять направление и скорость движения этих тел или приводить тело в состояние покоя.
- ребята слепили снеговика, а хулиганы его разрушили. Получается, что хулиганы приложили к снеговику свою силу, тем самым вызвали изменение формы снеговика;
- на дворе стояла тележка. Прохожий случайно задел её и тележка сдвинулась с места. Получается, что прохожий применил силу к тележке и вызвал её движение;
- далее тот же прохожий остановил тележку, чтобы она далеко не уехала. Получается, что прохожий применил силу, тем самым привел тележку в состояние покоя.
Сила является физической величиной — мерой воздействия на тело других тел. Сила обозначается заглавной латинской буквой F.
Что такое работа?
Работа — это количественная мера действия силы на тело. Работа зависит от количества силы, приложенной на тело и от направления этой силы, а также от перемещения данного тела.
Например, если мы попробуем сдвинуть шкаф с места и он сдвинется, то можно сказать, что мы совершили работу, поскольку сила, которую мы приложили, привела к тому, что шкаф совершил перемещение на некоторое расстояние.
Если же мы, к примеру, попробуем толкнуть стену, то стена с места не сдвинется, а значит и работа не будет совершена, поскольку сила была приложена, но эта сила не вызвала никакого перемещения стены.
Работа обозначается заглавной латинской буквой A.
Производительность
Производительностью называют работу, выполненную за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда. Производительность обозначается латинской буквой v
Рассмотрим следующий пример. Два пекаря пекли булочки. Первый пекарь испёк 40 булочек за 10 минут, а второй 15 булочек за 5 минут. Как узнать, кто из пекарей работал быстрее, первый или второй?
Работал быстрее тот, кто за одну минуту выпекает больше булочек. Говорят, что у него производительность больше. Для нахождения производительности предусмотрено следующее правило:
Чтобы найти производительность, надо выполненную работу разделить на время работы.
Также, можно воспользоваться формулой:
где v — производительность, A — выполненная работа, t — время работы.
Вернемся к нашей задаче. Зная правило или формулу нахождения производительности, можно определить сколько булочек приходится на одну минуту.
Найдём производительность первого пекаря. Разделим работу, которую он выполнил, на время которое он на нее затратил. Выполненная работа это количество испеченных им булочек, то есть 40, а время — 10 минут
40 : 10 = 4 булочки в минуту
Аналогично найдём производительность второго пекаря. Разделим 15 на 5
15 : 5 = 3 булочки в минуту
Первый пекарь в минуту выпекает больше булочек чем второй, значит его производительность выше. Отсюда делаем вывод, что работает он быстрее второго пекаря.
Также можно воспользоваться формулой нахождения производительности. В этом случае решение принимает следующий вид:
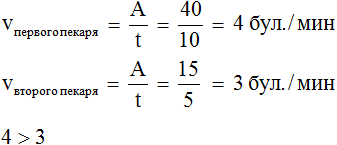
Под буквой v можно делать метки, указывающие для кого/чего мы находим производительность.
Задача 2. Тому нужно за 2 дня прочитать книгу, в которой 100 страниц. В первый день он читал 4 часа со скоростью 12 страниц в час. С какой скоростью ему надо читать оставшуюся часть книги, если у него есть на это 4 часа?
Узнаем сколько страниц Том прочитал в первый день. Он читал 12 страниц в час. Чтению в первый день он посвятил 4 часа, поэтому для нахождения количества прочитанных страниц в первый день, нужно 12 умножить на 4
12 × 4 = 48 страниц прочитано в первый день
Узнаем сколько страниц осталось прочесть. Вычтем из общего количества страниц ( 100 ) количество прочитанных страниц ( 48 )
100 − 48 = 52 страницы осталось прочесть
Осталось прочесть 52 страницы. Теперь найдем такую производительность, при которой Том сможет прочесть 52 страницы за 4 часа. Раскидаем 52 страницы на 4 часа поровну
52 : 4 = 13 страниц в час
Ответ: чтобы прочитать оставшуюся часть книги за 4 часа, Том должен читать ее со скоростью 13 страниц в час.
Замечание. В некоторых источниках слово «производительность» может быть заменено на слова «скорость», «эффективность», «продуктивность», «плодотворность».
Задача 3. Один насос работал 4 часа, выкачивая 158 вёдер воды в час, а другой — 3 часа, выкачивая 169 вёдер воды в час. Определить какой из насосов выкачал больше вёдер.
Решение
Определим сколько всего вёдер выкачал каждый насос по отдельности. Для этого умножим их производительность на время их работы:
158 в/ч × 4 = 632 вёдер выкачал первый насос
169 в/ч × 3 = 507 вёдер выкачал второй насос
Ответ: первый насос выкачала больше вёдер, чем второй.
Задача 4. За 2 часа насос выкачал 80 литров воды. Определить сколько литров он выкачает за 5 часов.
Решение
Сначала нужно определить сколько литров воды насос выкачивает за час. Для этого 80 литров разделим на 2 часа — получим 40 литров
80 : 2 = 40 литров в час
За один час насос выкачивает 40 литров воды. За 5 часов выкачает в пять раз больше
40 × 5 = 200 литров
Ответ: за 5 часов насос выкачает 200 литров воды.
Если известны производительность и время работы, то можно найти выполненную работу. Выполненная работа равна производительности умноженной на время работы:
A = v × t
Например, если производительность пекаря составляет 50 булочек в час, и он проработал 4 часа, то можно найти всю выполненную работу за эти четыре часа. Для этого производительность (50 бул/ч) нужно умножить на время его работы (4ч)
50 × 4 = 200 булочек

Если известны работа и производительность, то можно найти время работы. Время работы равно отношению выполненной работы к производительности:
Например, если в неделю бригада отстраивает 2 этажа, то можно узнать сколько недель потребуется для отстройки 8 этажей. Чтобы определить время отстройки восьми этажей, нужно выполненную работу (8 этажей) разделить на производительность (2 эт./нед):
Либо с помощью формулы, приведенной выше:
![]()

Если в неделю строится 2 этажа, то 8 этажей будет отстроено за четыре недели. В данном случае вся работа была равна восьми. Производительность была равна двум, поскольку по определению производительность есть работа, выполненная за единицу времени – в нашем случае два этажа за неделю.
Задача 6. Принтер работает с производительностью 70 стр./ч. Сколько страниц он напечатает за 5 часов?
Решение
Если в час принтер печатает 70 страниц, то за 5 часов он напечатает в 5 раз больше:
70 × 5 = 350 страниц
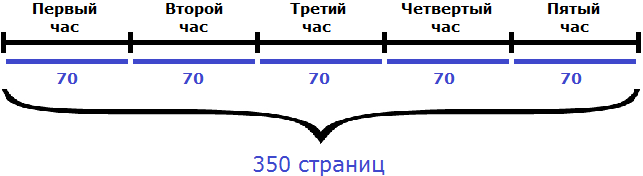
Также, решение можно записать с помощью формулы нахождения работы. В данном случае, количество напечатанных страниц являются выполненной работой:
A = v × t = 70 × 5 = 350 страниц
Задача 7. Принтер напечатал 350 страниц за 5 часов. С какой производительностью он работал?
Решение
Если в течении пяти часов принтер напечатал 350 страниц, то в течении часа он печатал . То есть работал с производительностью 70 страниц в час:
350 : 5 = 70 стр./ч.
Либо с помощью формулы нахождения производительности:
![]()
Задача 8. Принтер работал с производительностью 70 страниц в час и напечатал 350 страниц. Определить время работы принтера.
Решение
Выражение «работал с производительностью 70 страниц в час» означает, что в каждом часе принтер печатал по 70 страниц. И это продолжалось до тех пор, пока он не напечатал 350 страниц. Очевидно, что разделив 350 страниц по 70, мы определим время работы принтера, то есть узнаем сколько часов он работал
Либо с помощью формулы нахождения времени:
![]()
Задача 9. Машинистка в первый день напечатала 48 страниц рукописи, а во второй день — на 12 страниц больше, чем в первый. На всю работу в эти 2 дня она затратила 9 часов. Сколько часов работала она в каждый из этих дней, если производительность её не менялась ?
Решение
Определим сколько страниц напечатала машинистка во второй день. В условии сказано, что напечатала она на 12 страниц больше, чем в первый:
48 + 12 = 60 страниц во второй день.
Определим сколько страниц машинистка напечатала за два дня:
48 + 60 = 108 страниц за два дня.
На эту работу машинистка затратила 9 часов. Также сказано, что производительность её не менялась. Если мы разделим выполненную работу (108) на время выполнения (9), то определим производительность машинистки:
108 : 9 = 12 страниц в час.
Теперь мы можем определить сколько часов работала машинистка в каждый из двух дней. Для этого поочередно разделим выполненные работы в каждом из двух дней на производительность:
48 : 12 = 4 часа работала машинистка в первый день
60 : 12 = 5 часов работала машинистка во второй день.
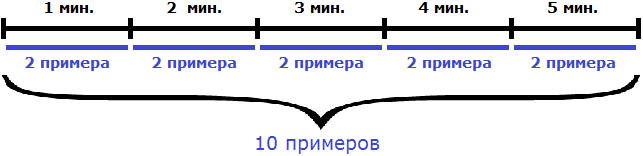
Задача 10. Джон решил 10 примеров за 5 минут. С какой производительностью он решал эти примеры?
10 примеров это выполненная Джоном работа. 5 минут — время работы. Разделим выполненную работу на время работы и определим производительность Джона:
10 : 5 = 2 примера в минуту.
Производительность Джона равна двум примерам в минуту.
Задача 11. Джон решил несколько примеров за 5 минут. С какой производительностью он решил эти примеры?
Это та же самая задача, что и предыдущая, но в ней работа не выражена каким-либо числом. Сказано лишь то, что Джон выполнил эту работу за 5 минут. Поэтому, конкретную производительность в такой задаче узнать нельзя. Но можно воспользоваться дробями. Обозначим выполненную работу через единицу. Тогда производительность работы Джона будет выражаться дробью – частью примеров, решенных за единицу времени. Если вы изучили задачи на дроби, то должны понимать о чем идёт речь.
Итак, обозначим выполненную работу через единицу:
Мы знаем, что для нахождения производительности, выполненную работу нужно разделить на время. Время работы у нас равно пяти минутам. Поэтому, единицу делим на пять минут:
Дробь выражает часть работы, выполненную Джоном за единицу времени. Если мы вернемся к предыдущей задаче, где выполненная работа была равна десяти примерам и найдем одну пятую от этой работы, то получим 2
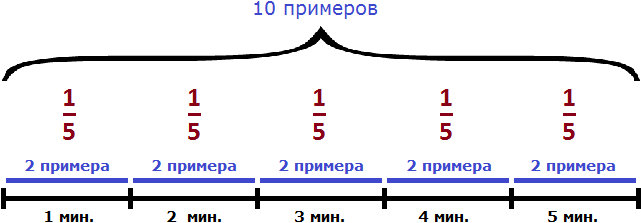
Выражать выполненную работу через единицу часто приходится при решении задач на совместную работу.
Задачи на совместную работу
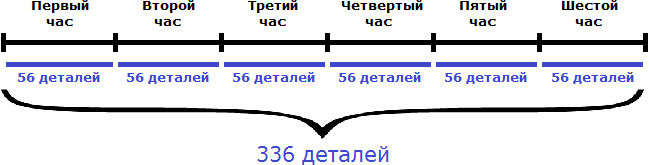
Задача 1. Первый мастер за 2 часа изготавливает 64 детали, а второй за 3 часа – 72 детали. За сколько часов они изготовят 336 деталей?
В данной задаче речь идет о совместной работе. Необходимо определить производительность обоих мастеров и найти время за которое они изготовят 336 деталей.
Для начала определим производительность первого мастера:
64 : 2 = 32 дет./час
Определим производительность второго мастера:
72 : 3 = 24 дет./час
Определим совместную производительность мастеров. Для этого сложим количество деталей, которые они изготавливают по отдельности за единицу времени. То есть сложим их производительности:
32 дет./час + 24 дет./час = 56 дет./час
Вместе за один час мастера изготавливают 56 деталей. Чтобы узнать за сколько часов они изготовят 336 деталей, нужно определить сколько раз 336 содержит по 56
336 : 56 = 6 часов
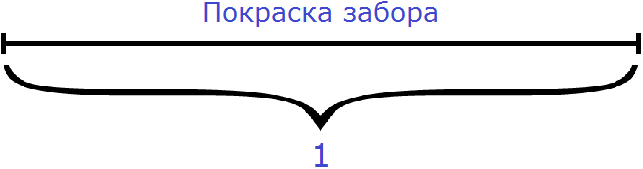
Задача 2. Первый мастер может покрасить забор за 20 минут, а второй мастер – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор?
Решение
В данной задаче, в отличие от предыдущей, работа не выражена каким-либо числом. Сказано лишь то, что эту работу первый мастер может выполнить за 20 минут, а второй за 30 минут.
В такой ситуации можно воспользоваться дробями. Мы можем обозначить всю работу (покраску забора) через единицу.
Итак, обозначим работу (покраску забора) через единицу:
Производительность первого мастера будет выражáться дробью . То есть за одну минуту он покрасит одну двадцатую часть забора. Единица это вся работа, а двадцать минут это время работы. Запишем производительность первого мастера с помощью формулы нахождения производительности:
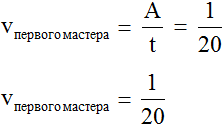

А производительность второго мастера будет выражáться дробью . То есть за одну минуту он покрасит одну тридцатую часть забора:
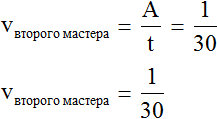
Определим общую производительность мастеров. Для этого сложим дроби, выражающие производительность первого и второго мастеров:
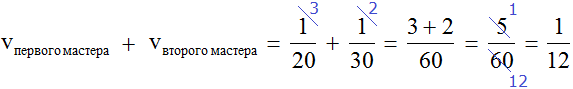
это дробь, выражающая общую производительность обоих мастеров. То есть за одну минуту мастера вместе покрасят часть забора.

Определим время за которое мастера покрасят забор вместе. Для этого воспользуемся формулой нахождения времени: разделим выполненную работу на общую производительность мастеров. Выполненная работа у нас выражена единицей, а производительность — дробью
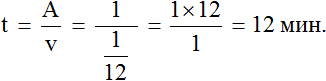
Ответ: работая вместе, мастера покрасят забор за 12 минут.
Задача 3. Первый рабочий может выполнить заказ за 8 часов, а второй за 6 часов. Два часа они работали вместе, а заканчивал работу один второй рабочий. Сколько времени потребовалось для выполнения этого заказа?
Решение
Обозначим всю работу через единицу
Тогда первый рабочий за один час может выполнить часть работы, а второй рабочий часть работы. А вместе за один час они могут выполнить часть работы
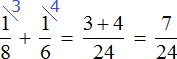
Рабочие работали вместе два часа, поэтому умножим часть работы, выполняемую ими за один час на 2:
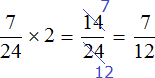
Остальную часть работы, а именно работы заканчивал один второй рабочий:
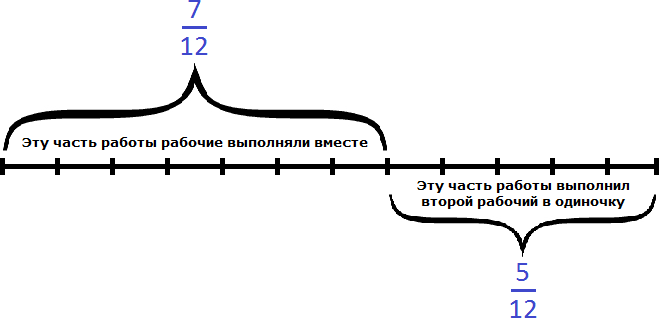
Второй рабочий за один час мог выполнить часть работы. Чтобы определить время за которое он завершил оставшуюся часть работы, воспользуемся формулой нахождения времени.
Переменная A теперь равна , переменная v —
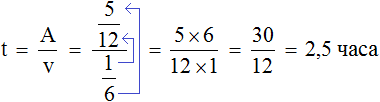
Теперь определим общее время заказа. Первые два часа рабочие работали вместе, остальную часть работы второй рабочий выполнил за два с половиной часа, отсюда имеем 4,5 ч.
Ответ: для выполнения заказа потребовалось 4,5 ч.
Задача 4. Одна труба наполняет бассейн за 6 ч, а другая – за 4 ч. За
сколько часов наполняют бассейн обе трубы, работая вместе?
Решение
Обозначим работу (наполнение бассейна) через единицу
Тогда первая труба за один час выполнит часть работы, а вторая труба — часть работы. Работая вместе за один час они выполнят часть работы:
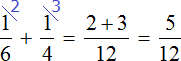
Определим время за которое обе трубы наполняют бассейн, работая вместе:
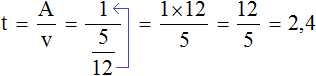
2,4 это два целых часа и четыре десятых часа
А четыре десятых часа это 24 минуты
60 мин. × 0,4 = 24 мин.
Ответ: работая вместе обе трубы наполнят бассейн за 2 ч 24 мин.
Задачи для самостоятельного решения
Задача 1. Первая бригада может выполнить некоторое задание за 12 часов, вторая – за 4 часа. За сколько часов они выполнят задание, если будут работать вместе?
Решение
Обозначим работу через единицу:
Тогда первая бригада за один час выполнит  часть работы, а вторая за один час
часть работы, а вторая за один час  часть работы. Их общая производительность равна сумме дробей
часть работы. Их общая производительность равна сумме дробей  и
и  :
:
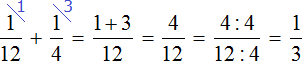
Определим время за которое обе бригады выполнят задание, работая вместе:
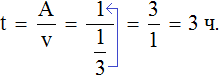
Ответ: обе бригады выполнят задание за 3 часа.
Задача 2. Лошадь съедает копну сена за 1 сутки, корова может съесть такую же копну за 3 суток, а овца за 6 суток. За какое время съедят эту копну лошадь, корова и овца вместе.
Решение
Работа в данном случае это съедание копны сена. Обозначим её через единицу:

Тогда производительность лошади будет выражáться единицей, производительность коровы — дробью , производительность овцы — дробью . Их совместная производительность равна следующей сумме:

Определим время, за которое лошадь, корова и овца съедят 1 копну сена:

Ответ: лошадь, корова и овца съедят 1 копну сена за суток или 16 часов.
Задача 3. Сосуд наполняется шлангом за 12 мин, а полный сосуд опорожняется при открытии крана за 20 мин. За какое время наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг?
Решение
Работа в данном случае это наполнение сосуда. Обозначим эту работу через единицу:
В условии сказано, что сосуд наполняется шлангом за 12 минут. Значит в минуту будет наполняться  часть сосуда. При этом сказано, что одновременно открыт кран сосуда и из него вытекает вода, которой наполняется сосуд. Вода, которая вытекает равна
часть сосуда. При этом сказано, что одновременно открыт кран сосуда и из него вытекает вода, которой наполняется сосуд. Вода, которая вытекает равна  части сосуда, поскольку в условии сказано, что полный сосуд опорожняется за 20 минут.
части сосуда, поскольку в условии сказано, что полный сосуд опорожняется за 20 минут.
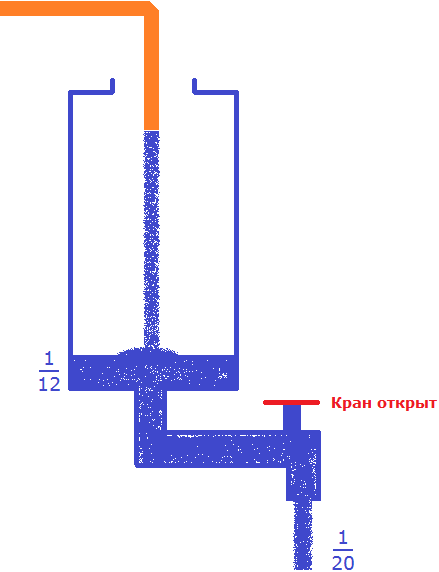
В сосуд поступает воды больше, чем вытекает. Дробь  больше, чем
больше, чем  .
.

Несмотря на то, что часть поступающей в сосуд воды будет вытекать, с каждой минутой сосуд будет пополняться на определенную часть. Узнаем, что эта за часть. Для этого из поступающей части вычтем ту часть, которая вытекает:
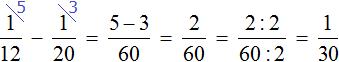

Каждую минуту сосуд будет наполняться на .
Определим время за которое наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг:
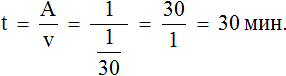
Ответ: если одновременно открыть кран и вливать в пустой сосуд воду через шланг, то он наполнится за 30 минут.
Задача 4. Через первую трубу бассейн можно заполнить за 20 ч, через вторую за 30 ч. Какая часть бассейна заполнится через обе трубы за 1 ч?
Решение
Работа в данном случае это заполнение бассейна. Обозначим эту работу через единицу:
Производительность заполнения бассейна через первую трубу будет выражáться дробью  , через вторую трубу — дробью
, через вторую трубу — дробью  . Совместная производительность будет выражáться дробью
. Совместная производительность будет выражáться дробью 

Производительность по определению есть работа, выполненная за единицу времени. Значит дробь является ответом к задаче, поскольку нас интересовало какая часть бассейна заполнится через обе трубы за 1 час. Это можно проверить, воспользовавшись формулой нахождения работы. Переменная v у нас имеет значение , а переменная t равна единице (одному часу). Формула нахождения работы позволит нам определить какая часть работы будет выполнена за 1 час:
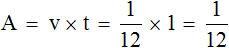

Ответ: за один час заполнится часть бассейна.
Задача 5. На прокладку траншеи требуется затратить 10 ч. Экскаватор проработал 8 ч, после чего ему осталось пройти 50 м. Найти общую длину траншеи.
Решение
В задаче подразумевается, что экскаватор работал с одинаковой производительностью на протяжении всей работы. На работу требовалось затратить 10 ч. Проработано было 8 ч. Значит осталось еще 2 часа. На 2 часа приходятся оставшиеся 50 метров траншеи. Если разделить 50 метров на 2, то можно определить сколько метров экскаватор прокладывает за один час:
В час экскаватор прокладывал 25 метров. Работал он 10 часов. Умножим 25 на 10, мы определим общую длину траншеи:
Ответ: общая длина траншеи составляет 250 м.
Задача 6. Ванна заполняется холодной водой за 6 мин 40 с, горячей – за 8 мин. Кроме того, если из полной ванны вынуть пробку, вода вытечет за 13 мин 20 с. Сколько времени понадобится, чтобы наполнить ванну полностью, при условии, что открыты оба крана, но ванна не заткнута пробкой?.
Решение
Для удобства переведем время данное в задаче в секунды
6 мин 40 с = 400 с
8 мин = 480 с
13 мин 20 с = 800 с
Обозначим заполнение ванны через единицу:
Производительность первого крана будет выражáться дробью  , производительность второго крана — дробью
, производительность второго крана — дробью  . Совместная производительность обоих кранов равна сумме дробей
. Совместная производительность обоих кранов равна сумме дробей  и
и 
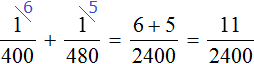
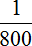
Одновременно с открытыми двумя кранами, вынута пробка из ванны. Поэтому часть поступающей в ванну воды сразу выходит через слив. Эта часть будет выражáться дробью .
С каждой секундой ванна будет пополняться на определенную часть воды. Узнаем какая это часть. Для этого из поступающей части воды вычтем ту часть, которая вытекает через слив.

Определим сколько времени понадобится, чтобы наполнить ванну:
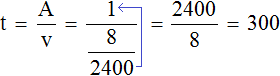
Ванна наполнится за 300 секунд. Поскольку задача завершена, секунды можно обратно перевести в минуты. Триста секунд это пять минут:
Ответ: ванна заполнится за 5 мин.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор
17 thoughts on “Производительность”
Elchin :
Спасибо за прекрасные уроки. Жду с нетерпением уроки на уравнениe. Знаю,знаю у вас пока времени нет =)
Одно замечание- некоторые действительно сложные примеры Вы недостаточно разъясняете…простое разжёвываете слишком, а сложное недостаточно…
А в целом большое спасибо.
Два экскаватора работая одновременно могут вырыть котлован за 6 ч 40 мин
Два экскаватора,работая одновременно с одинаковой производительностью,могут вырыть котлован за 10,5 часов. За сколько времени они сделают эту работу,работая одновременно,если один из них увеличит свою производительность за 10%?
Голосование за лучший ответ
Пусть х — производительность одного экскаватора, двух — 2х
Объем котлована — 2х*10,5.
2х+1/10х -производительность двух экскавторов при увеличении на 10% производительности одного из экскаваторов.
2х*10,5 :(2х+1/10х) = 10 (час).
Два экскаватора, работая одновременно, могут выполнить задание за 6 часов. Первый экскаватор, работая отдельно может
выполнить это задание на 5 часов быстрее, чем второй экскаватор . За сколько времени может выполнить задание первый экскаватор, работая отдельно?
Ответ или решение 1
Предположим, что всю работу можно записать как целое число равное 1.
В таком случае, работая вместе, за 1 час экскаваторы сделают:
1 / 6 = 1/6 часть работы.
Запишем время работы первого экскаватора как неизвестное число х.
В таком случае, время работы второго будет равно: х + 5 часов.
Сумма их продуктивности работы будет равна 1/6.
Получим уравнение:
1 / х + 1 / (х + 5) = 1/6.
Освобождаемся от знаменателя.
6 * х + 6 * х + 30 = х^2 + 5 * x.
— х^2 + 12 * х — 5 * х + 30 = 0.
х^2 — 7 * х — 30 = 0.
Находим Дискриминант.
Д = 7 * 7 — 4 * 1 * (-30) = 49 + 120 = 169.
Д = 13.
х1 = (7 + 13) / 2 = 20 / 2 = 10 часов (Скорость первого экскаватора.)
х2 = (7 — 13) / 2 = — 3 (Данное число отрицательное.)
Два экскаватора работая вместе могут вырыть яму за 6 часов, Первый экскаватор, работая отдельно может вырыть яму на 9
Обозначим через х производительность первого экскаватора, а через у производительность второго экскаватора.
По условию задачи, два экскаватора, работая вместе, могут вырыть яму за 6 часов, следовательно, можем записать следующее соотношение:
Также известно, что работая отдельно, первый экскаватора может вырыть яму на 9 часов быстрее, чем второй, следовательно, можем записать следующее соотношение:
Решаем полученную систему уравнений. Подставляя во второе уравнение значение у = 1/6 — х из первого уравнения, получаем:
Задание 11
Два экскаватора, работая совместно, могут вырыть котлован за 48 ч. Если первый проработает 40 ч, а второй – 30 ч, то будет выполнено 75% всей работы. За какое время может вырыть котлован второй экскаватор, работая отдельно?
Пусть производительность первого экскаватора (x ,) в второго (y.) Из первого условия составим первое уравнение и выразим из него производительность первого экскаватора ( =48 Rightarrow x= -y.)
Составим второе уравнение из второго условия (x+30y=0.75.)
Подставим найденный (x) во второе уравнение и найдем искомое время ( =120) часов.
Два экскаватора различной мощности роют котлован. Работая отдельно, первый может вырыть котлован за 10 дней, второй — за 15 дней. За сколько дней они выроют котлован, работая совместно?
Найди верный ответ на вопрос ✅ «Два экскаватора различной мощности роют котлован. Работая отдельно, первый может вырыть котлован за 10 дней, второй — за 15 дней. За . » по предмету Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Новые вопросы по математике
2 тыс=. Дес 2 дес. тыс.=тысяч. 5 сот тысяч=дес. тыс 3 дес. тыс=сот тысяч 10 дес=ед 20 дес. тыс=сот тысяч
Рівняння 14010 — z = 3815
В треугольнике авс сторона ав=корень из 43, вс=корень из 59, ас=4. Найдите величину наибольшего угла
Сколько существует различных расположений 15 монеток, в которых нет 2 подряд идущих орлов?
Стороны треугольника равны 3/8 м, 1/2 м, 5/6 м. найти периметр
Главная » ⭐️ Математика » Два экскаватора различной мощности роют котлован. Работая отдельно, первый может вырыть котлован за 10 дней, второй — за 15 дней. За сколько дней они выроют котлован, работая совместно?
Два экскаватора, работая вместе, могут вырыть яму за 6 ч?
Два экскаватора, работая вместе, могут вырыть яму за 6 ч.
Первый экскаватор, работая отдельно, может вырыть яму за 9 ч быстрее, чем второй.
За сколько часов может вырыть яму второй экскаватор ?
Ответить на вопрос Для ответа на вопрос необходимо пройти авторизацию или регистрацию.

Кира20041 20 янв. 2021 г., 13:59:55
Пусть скорость копания первого — х, а второго у
тогда работу (принимая ее за 1) они могут выполнить соответственно за 1 / х (это первый) либо 1 / у( второй) часов.
Первый быстрее второго на 9 часов.
(второй дольше) т.
Е. 1 / у — 1 / х = 9
если работают вместе, то скорость будет (х + у), и работу выполнят за 1 / (х + у) = 6 часов.
Решая систему двух ур — ий, получаем
у = 1 / 18 — это скорости работ, а работа второго будет 18 часов.

Liberty00 28 апр. 2021 г., 15:27:06 | 10 — 11 классы
Пять рабочих вырыли яму глубиной 5 метров за пять часов?
Пять рабочих вырыли яму глубиной 5 метров за пять часов.
Сколько рабочих понадобится, чтобы вырыть яму глубиной 100 метров за сто часов.

Сверик14 8 мар. 2021 г., 20:02:34 | 5 — 9 классы
Два экскаватора, работая одновременно, могут выполнить задание за 3, 75 часа?
Два экскаватора, работая одновременно, могут выполнить задание за 3, 75 часа.
Первый экскаватор, работая отдельно может выполнить это задание на 4 часа скорее, чем второй экскаватор .
За сколько времени может выполнить задание первый экскаватор, работая отдельно?

Засеряdrgsdg 10 мая 2021 г., 08:23:03 | 5 — 9 классы
Два экскаватора, работая одновременно, могут выполнить задание за 8 часов?
Два экскаватора, работая одновременно, могут выполнить задание за 8 часов.
Первый экскаватор, работая отдельно может выполнить это задание на 12 часов быстрее, чем второй экскаватор .
За сколько времени может выполнить задание первый экскаватор, работая отдельно?

Рызгуль1 23 мая 2021 г., 20:58:22 | 5 — 9 классы
Два экскаватора, работая одновременно, могут выполнить задание за 6 часов?
Два экскаватора, работая одновременно, могут выполнить задание за 6 часов.
Первый экскаватор, работая отдельно может выполнить это задание на 5 часов быстрее, чем второй экскаватор .
За сколько времени может выполнить задание первый экскаватор, работая отдельно?

Nastya151515 2 апр. 2021 г., 05:02:10 | 5 — 9 классы
Первый экскаватор может вырыть траншею за 7 ч, а второй за 5 ч?
Первый экскаватор может вырыть траншею за 7 ч, а второй за 5 ч.
Какую часть траншеи останется вырыть через 1 час совместной работы двух экскаваторов?

Светлячок 18 июн. 2021 г., 16:15:26 | 5 — 9 классы
Два экскаватора, работая одновременно, могут выполнить задание за 6 часов?
Два экскаватора, работая одновременно, могут выполнить задание за 6 часов.
Первый экскаватор, работая отдельно может выполнить это задание на 5 часов быстрее, чем второй экскаватор .
За сколько времени может выполнить задание первый экскаватор, работая отдельно?
Ответ : Первый экскаватор, работая отдельно может выполнить задание за ч.
ТОЛЬКО ОТВЕТ ПОЖАЛУЙСТА!

Evg1811 22 мая 2021 г., 01:56:53 | 5 — 9 классы
Помогите пожалуйста решить задачу с иксом (но без процентов)Один экскаватор может вырыть траншею за 30ч, другой — — за 20ч?
Помогите пожалуйста решить задачу с иксом (но без процентов)
Один экскаватор может вырыть траншею за 30ч, другой — — за 20ч.
Первый проработал 9ч, а потом второй закончил работу.
За сколько часов была выполнена работа?
Пожалуйста помогите : с.

Aleks5454hdhvdh 8 июл. 2021 г., 07:52:24 | 5 — 9 классы
3 экскаватора различной мощности могут вырытькотлован, работая отдельно : первый — 10дней , второй — за12дней, в третий — за 15дней?
3 экскаватора различной мощности могут вырытькотлован, работая отдельно : первый — 10дней , второй — за12дней, в третий — за 15дней.
За сколько времени они могут вырыть котлован, работая совместно?

Syriusblack1994 6 мая 2021 г., 14:28:29 | 5 — 9 классы
Два экскаватора работая одновременно могут выполнить определенный объем земляных работ за 3 часа 45 минут 1 экскаватора работая отдельно может выполнить этот объем работ за 6 часов За сколько часов мо?
Два экскаватора работая одновременно могут выполнить определенный объем земляных работ за 3 часа 45 минут 1 экскаватора работая отдельно может выполнить этот объем работ за 6 часов За сколько часов может выполнить всю эту работу другой экскаватор.

1234567891092 1 мая 2021 г., 18:50:27 | 5 — 9 классы
Два экскаватора могут вырыть траншею за 10?
Два экскаватора могут вырыть траншею за 10.
За какое время смогут вырыть эту траншею 5 таких же экскаваторов.
Если вам необходимо получить ответ на вопрос Два экскаватора, работая вместе, могут вырыть яму за 6 ч?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Математика вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Ananimnocom 18 сент. 2021 г., 15:17:29
Шахо блин шо эта за хек.

Hgf543 18 сент. 2021 г., 15:15:34
|2 — ( — 3)| — |3 — 6| + x = 0 ; |5| — | — 3| + x = 0 ; 5 — 3 + x = 0 ; 2 + x = 0 ; x = — 2. Ответ : — 2 (в).

Mariy1200Siv 18 сент. 2021 г., 15:14:25
Х ч. — ехал на теплоходе х + 3 ч — ехал на поезде 25х км — проехал на теплоходе 60 * (х + 3) км — ехал на поезде 25х + 60(х + 3) = 605 25х + 60х + 180 = 605 85х = 605 — 180 х = 425 : 85 х = 5 ч — ехал на теплоходе 5 + 3 = 8 ч — ехал на поезде Ответ .

Sgondar 18 сент. 2021 г., 15:12:08
Ответ : 4 см сторона квадрата.

80936760037 18 сент. 2021 г., 15:11:17

Gubarkova01 18 сент. 2021 г., 15:11:01
4 9 / 10 1 567 / 1000 0 43 / 1000 5 6 / 10 8 95 / 100 0 26 / 100 0 88 / 10000 12 18 / 1000.

ЛапуляЯ98 18 сент. 2021 г., 15:02:35
Умножение, потому что первые действия всегда в скобках) 1) + 2) — 3) *.

Pavlovao1701 18 сент. 2021 г., 15:01:21
1)2(х + 5) = 12 х + 5 = 12 : 2 х + 5 = 6 х = 6 — 5 х = 1 2(1 + 5) = 12 2)84 : (х — 3) = 42 х — 3 = 84 : 42 х — 3 = 2 х = 2 + 3 х = 5 84 : (5 — 3) = 42 3)3(х + 4) = 33 х + 4 = 33 : 3 х + 4 = 11 х = 11 — 4 х = 7 3(7 + 4) = 33 4)45 : (х — 5) = 15 х — 5 ..

Slastenastena 18 сент. 2021 г., 15:00:20
На седьмом : на этом этаже квартиры 31 — 35.

Rsacha 18 сент. 2021 г., 15:00:18
32 : 5 = 6 (ост. 2) — шесть этажей и еще две квартиры остается. Значит квартира №32 на 7 этаже.
Два экскаватора, работая вместе, могут вырыть котлован за 48 ч. За какое время может вырыть котлован каждый из них в отдельности, если второй работает в
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
два экскаватора,работая одновременно,могут вырыть котлован за 4 часа
два экскаватора,работая одновременно,могут вырыть котлован за 4 часа.Один первый экскаватор затратит на эту работу на 6 часов больше чем 2.За какое время может вырыть котлован каждый экскаватор,работая отдельно?
(Х+Х+6)=4, 2х+6=4, 2х=10, х=5, х+6=11
ответ? 1за 5ч, 2 за11
первый- за 5 час; второй- за -1 час
Чепуху тебе «ответчики» городят. Первый экскаватор выроет за 12 часов, второй за 6. Обозначим время, за которое первый экскаватор выроет котлован за х часов, тогда второй котлован выроет за (x-6) часов. За 1 час первый экскаватор выкопает 1/x часть котлована, а второй за 1 час выкопает 1/(x-6) часть котлована. А вместе за час по условию они выкопают 1/4 часть котлована (поскольку целиком они выкопают его вместе за 4 часа) . Имеем уравнение:
1/x+1/(x-6)=1/4
Квадратное уравнение:
4*x-24+4*x=x^2-6*x
Приводим подобные:
x^2-14*x+24=0
x1=12 (часов)
x2=2 (часа) — посторонний корень, поскольку в этом случае время, за которое второй экскаватор выкопает котлован, будет отрицательным (2-6=-4), что не имеет физического смысла.
Итак, первый экскаватор выкопает котлован за 12 часов, а второй за 12-6=6 часов
Ответ: Первый за 12, второй за 6 часов.
Примечание: Учитесь, дети, решать подобные задачи. Они типичны!
Два экскаватора работая одновременно могут вырыть котлован за 6 ч 40 мин
УПС, страница пропала с радаров.
Вам может понравиться Все решебники

Вербицкая, Гаярделли, Редли


Рыбченкова, Александрова, Загоровская

Юлия Ваулина, Джунни Дули


Баранова, Афанасьева, Михеева
Главная задача сайта: помогать школьникам и родителям в решении домашнего задания. Кроме того, весь материал совершенствуется, добавляются новые сборники решений.
Читайте также:
- Дом построил а жить не стал
- В какие сроки проводится текущий ремонт запорной арматуры и компенсаторов
- Браширование доски своими руками
- В повести котлован строительство
- Бытовка из сэндвич панелей своими руками
Математика по полочкам
В таких задачах всегда присутствуют одни и те же величины, их три:
— первая величина — это время, за которое выполняется та или иная работа. Обозначают время буквой t.
— вторая величина — объём работы: сколько сделано деталей, налито воды, вспахано полей и так далее. Обозначим объем буквой О.
— третья величина — производительность. По сути, это скорость работы. Обозначим производительность буквой П.
Скорость любой работы, т.е. производительность можно определить, как объём работы, сделанной за какое-то время.
Получим формулу для производительности: П = О : t.
Пример. Токарь делает 5 деталей в час. Сколько деталей он сделает за 7 часов?
5 деталей в час — производительность
7 часов — время работы
Найти объем.
5 · 7 = 35.
Ответ: 35 деталей.
Пример. Токарь делает 5 деталей в час. Ему нужно сделать 20 деталей. За какое время он выполнит эту работу?
Известны объем и производительность, найти время.
20 : 5 = 4.
Ответ: 4 часа
Пример. Красная Шапочка и Волк очень любят пирожки. Волк может съесть 24 пирожка за 4 часа, а Красная Шапочка — 35 пирожков за 7 часов. У Волка в корзинке 30 пирожков, а у Красной Шапочки — 20. Кто съест свои пирожки раньше, если они начали есть одновременно?
Определим производительности Волка и Красной Шапочки. Волк съест 24 пирожка (объём работы) за 4 часа (время). Значит, его производительность: П = О:t = 24:4 = 6 пирожков в час.
Производительность Красной Шапочки: П = О:t = 35:7 = 5 пирожков в час.
Посчитаем сколько времени затратит каждый на свои пирожки.
У Волка 30 пирожков. Значит, затратил времени: t = О:П= 30:6 = 5 часов.
Красная Шапочка потратила на свои 20 пирожков: t = О:П = 20:5 = 4 часа.
Красная Шапочка опередила Волка на один час.
Ответ: Красная Шапочка.
Как определить производительность в следующих задачах:
— труба заполняет бассейн за 3 часа. (объем работы — бассейн — 1 бассейн);
— бригада строителей строит дом за 150 дней. (объем работы — дом — 1 дом);
— трактор вспахивает поле за 12 часов. (объем работы — поле — 1 поле).
Следовательно, в задачах объем работы равен 1.
Задачи на совместную работу
Совместная работа возникает, когда несколько человек (бригад, насосов, тракторов и т.д.) выполняют одну и ту же работу вместе, причем они работают с разными скоростями.
Пример. Одна труба может наполнить бассейн за четыре часа. Вторая — за шесть часов. За какое время заполнится бассейн, если обе трубы включить одновременно?
Так как трубы работают вместе, складывают их производительности.
Для первой трубы, которая заполняет 1 бассейн за 4 часа: П = О:t = 1:4, т.е. за час первая труба заполнит 1/4 бассейна.
Для второй трубы: П = О:t = 1:6, т.е. вторая труба заполнит за час 1/6 бассейна.
Вместе, при совместной работе, трубы заполнят за час: 1/4 + 1/6 = 5/12 — две трубы за 1 час.
Объём работы 1 бассейн. Совместная производительность 5/12 бассейна в час.
t = О:П = 1 : 5/12 = 12/5 = 2,4 (ч.)
Ответ:2,4 часа.
УПРАЖНЕНИЯ
1. а) Одна труба заполняет бассейн за 3 ч, а вторая — за 5 ч. За какое время заполнится бассейн, если будут работать две трубы одновременно? Выберите правильное значение:
1) (3+5):2; 2) 1: (3+5); 3) 1: (1/3+1/5).
б) Один насос заполняет бак за 4 ч, а второй — за 2 ч. За какое время заполнится бак, если будут работать два насоса одновременно? Выберите правильное значение:
1) (4+2):2; 2) 1: (1/4+1/2) ; 3) 1: (4+2).
Решение:
а) Производительность первой трубы — 1/3, производительность второй трубы — 1/5. Общая производительность — 1/3+1/5. Для нахождения затраченного времени при совместной работе разделим объем работы -1 на производительность: 1:(1/3+1/5).
Ответ: 3.
2. а) Два строителя вместе сложили стену за 10 дней, один из них мог бы выполнить эту работу за 16 дней. За сколько дней может выполнить эту работу второй? Выберите правильное значение:
1) 1: (1/10+1/16); 2) 1: (1/10-1/16); 3) 1: (16-10).
б) Одна наборщица может набрать рукопись за 12 ч, а две, работая вместе, — за 8 ч. За сколько часов выполнит эту работу вторая наборщица? Выберите правильное значение:
1)1: (1/8-1/12); 2) 1: (1/12+1/8); 3) 1: (12-8).
Решение:
а) Производительность первого строителя — 1/16, о бщая производительность — 1/10. Производительность второго строителя — 1/10-1/16. Для нахождения затраченного времени вторым строителем разделим объем работы -1 на производительность: 1:(1/10-1/16).
Ответ: 2.
3. а) Папа выполняет всю работу за 4 ч, а его сын— за 7 ч. Какую часть работы они сделают вместе за 1 ч?
б) Мама выполняет всю работу за 1 ч, а дочь эту же работу выполняет за 2 ч. Какую часть работы они сделают вместе за 1 ч?
Решение:
а) Производительность папы — 1/4, производительность сына — 1/7. Производительность общая: 1/4+ 1/7=11/28 всей работы за 1 час.
Ответ: 11/28 работы.
4. а) При одновременной работе 6 комбайнов уберут все поле за 14 ч. За сколько часов уберут поле 8 комбайнов?
б) При одновременной работе 7 комбайнов уберут поле за 14 ч. За сколько часов уберут поле 10 комбайнов?
Решение:
а) 1) 6*14=84 (ч) — понадобится одному комбайну, чтобы убрать все поле.
2) 84 : 8= 10,5 (ч) — понадобится 8 комбайнам, чтобы убрать все поле.
Ответ: 10,5 часов
5. а) 18 студентов, работая по 6 ч в день, прополют все поле все поле. Сколько понадобится студентов, чтобы прополоть это поле за то же время, если они будут работать по 9 ч в день?
б) 12 студентов, работая по 8 ч в день, соберут все яблоки в саду. Сколько понадобится студентов, чтобы убрать все яблоки в этом саду за то же время, если они будут работать по б ч в день?
Решение:
а) 1) 6*18=108 (ч) — понадобится одному студенту, чтобы прополоть все поле.
2) 108 : 9= 12(ст.) — понадобится, чтобы прополоть все поле, работая по 9 ч в день.
Ответ: 12 студентов.
6. а) Производительности дочери и мамы относятся как 2:3. Работая вместе, они прополют огород за 12 ч. За сколько часов прополет огород каждая, работая отдельно?
б) Производительности труда папы и сына относятся как 3 : 5. Работая вместе, они выполнят работу за 15 ч. За сколько часов каждый справится с данной работой, работая отдельно?
Решение:
а) Пусть х — коэффициент пропорциональности, тогда производительность дочери — 2х, а мамы — 3х. Производительность при совместной работе 2х+3х=5х. Объем работы равен 12*5х=60х.
1) 60х:2х=30 (ч) — затратит дочь.
2) 60х:3х=20 (ч) — затратит мама.
Ответ: 30 часов; 20 часов.
7. а) Заказ на печать учебников типография должна была выполнить по плану за 15 дней. Но уже за три дня до срока типография выполнила план, так как печатала ежедневно по 2 тыс. учебников сверх плана. Сколько учебников напечатала типография?
б) Заказ на выпуск станков завод должен был выполнить за 30 дней. Но за три дня до срока завод выполнил заказ, так как выпускал ежедневно по 3 станка сверх плана. Сколько станков выпустил завод?
Решение:
а) Пусть х учебников в день типография должна была печатать по плану, но печатала х+2000 учебников день.
1) 15-3=12 (дн.) — потратила типография на заказ.
15х — количество заказанных учебников, 12(х+2000) — количество напечатанных учебников. Эти количества равны. Составим и решим уравнение:
15х=12(х+2000),
15х=12х+24000,
3х=24000,
х=8000 (м.) — в день должна была печатать типография.
2) 8000*15=120000 (м.) — напечатала типография.
Ответ: 120000 учебников.
8. а) При совместной работе двух погрузчиков железнодорожный состав был загружен за 4 ч 12 мин. Сколько времени потребуется на загрузку такого же железнодорожного состава каждым погрузчиком, если одним из погрузчиков железнодорожный состав можно загрузить на 8 ч быстрее, чем другим?
б) При совместной работе двух кранов работа была выполнена за 2 ч 6 мин. Сколько времени потребуется для выполнения этой работы каждым краном, если один может выполнить ее на 4 ч быстрее другого?
Решение:
а) Пусть х — время загрузки состава первым погрузчиком, тогда х+8 — время загрузки состава вторым погрузчиком.
Производительность первого погрузчика — 1/х, второго погрузчика — 1/(х+8). Совместная производительность 1/х+1/(х+8)=(2х+8)/(х(х+8)).
Время совместной работы равно 1 : (2х+8) /(х(х+8))=х(х+8)/(2х+8).
По условию время равно 4 ч 12 мин = 4,2 ч. Составим и решим уравнение:
х(х+8)/(2х+8)=4,2,
х(х+8)=4,2(2х+8),
х 2 +8х-8,4х-33,6=0,
х 2 -0,4х-33,6=0,
D=( 11,6) 2
х1=6 (ч) — понадобится первому погрузчику, х2=(0,4-11,6):2=-5,6 — не подходит по условию задачи.
1) 6+8=14 (ч) — понадобится второму погрузчику.
Ответ: 6 часов, 14 часов.
9. а) Бассейн наполняется через две трубы за 6 ч. Через первую трубу бассейн наполняется на 5 ч быстрее, чем через вторую. За какое время может быть наполнен бассейн через каждую трубу в отдельности?
б) Бак наполняется через две трубы за 2 ч. Через первую трубу бак наполняется на 3 ч быстрее, чем через вторую. За какое время может быть наполнен бак через каждую трубу в отдельности? (№ 6.4.30 [7])
Решение:
а) Пусть х — время заполнения первой трубой, тогда х+5 — время заполнения второй трубой.
Производительность первой трубы 1/х, второй трубы 1/(х+5). Совместная производительность 1/х+1/(х+5)=(2х+5)/(х(х+5)).
Время совместной работы равно 1 : (2х+5) /(х(х+5))=х(х+5)/(2х+5).
По условию время равно 6 ч. Составим и решим уравнение:
х(х+5)/(2х+5)=6,
х(х+5)=6(2х+5),
х 2 +5х-12х-30=0,
х 2 -7х-30=0,
D=( 13) 2
х1=10 (ч) — понадобится первой трубе, х2=(7-13):2=-3 — не подходит по условию задачи.
1) 10+5=15 (ч) — понадобится второй трубе.
Ответ: 10 часов, 15 часов.
10. а) Двое плиточников облицевали стены за 12 ч. Если бы сначала первый облицевал половину стен, а затем второй — вторую половину, то облицовка была бы выполнена за 25 ч. За какое время мог бы облицевать стену каждый плиточник в отдельности?
б) Двое каменщиков сложили стену за 6 ч. Если бы сначала первый выложил половину стены, а затем второй — вторую половину стены, то вся стена была бы сложена за 12,5 ч. За какое время мог бы сложить эту стену каждый каменщик в отдельности?
Решение:
а) Пусть первый работал х часов, второй — у часов. Производительность первого 1/х, второго 1/у. При совместной работе их время равно 1: (1/х+1/у) =12.
Если первый и второй делают по половине работы, то их время равно 0,5:(1/х) +0,5:(1/у)=25. Решим систему из двух уравнений:
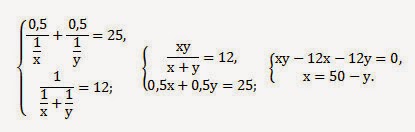
(50-у)у-12(80-у)-12у=0,
50у-у 2 -600+12у-12у=0,
у 2 -50у+600=0
D=( 10) 2
у1=20 (ч) — работал второй, х1=50-20=30 (ч) — работал первый.
у2=30 (ч) — работал второй, х1=50-30=20 (ч) — работал первый.
Ответ: 20 часов, 30 часов.
11. а) Рабочий копал траншею. Когда он проработал 7 ч, к нему присоединился второй рабочий. Вместе они проработали 2 ч. За сколько часов может выкопать траншею каждый рабочий, работая отдельно, если первому нужно на это на 4 ч больше, чем второму?
б) Один рабочий работал 9 ч, после чего к нему присоединился другой рабочий. После 7 ч совместной работы они выполнили всю работу. За сколько часов мог бы выполнить работу каждый рабочий, работая самостоятельно, если первому нужно для этого на 3 ч больше, чем второму?
Решение:
а) Пусть х — время работы первого, тогда х-4 — время работы второго.
Производительность первого — 1/х, второго — 1/(х-4).
Объем работы первого — 1/х*(7+2), объем работы второго — 1/(х-4)*2. Весь объем равен 1.
Составим и решим уравнение:
9/х + 2/(х-4)=1,
11х-36=х(х-4),
х 2 -15х+36=0,
D=( 9) 2
х1=3 (ч) — понадобится первому, 1) 3-4=-1(ч) — не подходит по условию задачи.
х2=12 ( ч) — понадобится первому, 2) 12-4=8 (ч) — понадобится второму.
Ответ: 12 часов, 8 часов.
12. а) Двое рабочих выполняют некоторую работу. После 45 мин совместной работы первый был переведен на другую работу и второй рабочий закончил оставшуюся часть работы за 2 ч 15 мин. За какое время мог бы выполнить всю работу каждый рабочий в отдельности, если известно, что второму для этого понадобится на 1 ч больше, чем первому? (№6.5.34 [7])
б) Бассейн может наполняться водой из двух кранов. Если открыть первый кран на 10 мин, а второй — на 20 мин, то бассейн будет наполнен. Если первый кран открыть на 5 мин, а второй — на 15 мин, то заполнится — бассейна. За какое время из каждого крана в отдельности может заполниться весь бассейн?
Решение:
а) Пусть х — время первого, тогда х+1 — время второго. Производительность первого 1/х, производительность второго 1/(х+1). Вместе они работали 45 мин=0,75 ч и выполнили (1/х + 1/(х+1)) * 0,75 часть работы. Второй за 2ч 15 мин=2,25 ч выполнил 1/(х+1)*2,25 часть работы. Составим и решим уравнение:
(1/х + 1/(х+1)) * 0,75 + 1/(х+1)*2,25 =1,
4х 2 -11х-3=0,
D=( 13) 2
х1=3 (ч) — понадобится первому,
х2=(11-13):2= -1 не подходит по условию задачи.
1) 3+1=4 (ч) — понадобится второму.
Ответ: 3 часа, 4 часа.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Два экскаватора различной мощности роют котлован. Работая отдельно, первый может вырыть котлован за 5 дней, второй — за 7 дней. За сколько дней они выроют котлован, работая совместно? Выберите правильное значение:
1) (7+5):2; 2) 1: (7+5); 3) 1: (1/7+1/5).
2. Одна из труб может наполнить бассейн за 3 ч, вторая — за 5 ч. За сколько часов наполнится бассейн, если открыть сразу две трубы? Запишите выражение для решения задачи.
3. Два экскаватора роют траншею. Работая отдельно, первый может вырыть траншею за 10 дней, второй — за 16 дней. За сколько дней они выроют траншею, работая совместно?
4. Водоем заполняется первой трубой за 5 ч, а второй трубой за 4 ч. За сколько часов наполнится водоем, если будут одновременно работать две трубы?
5. Две наборщицы должны были набрать по 120 страниц каждая. Вторая наборщица набирала за 1 ч на 5 страниц меньше, чем первая, поэтому закончила работу на 2 ч позже. Сколько страниц в час набирала первая наборщица?
6. Две бригады рабочих должны по плану изготовить 240 деталей. Первая бригада работала 6 ч, а вторая — 5 ч. Сколько деталей в час изготавливала каждая бригада, если первая делала на 4 детали в час меньше, чем вторая?
7. По плану колхоз каждый день должен был засевать по 20 га. Начав сев, колхоз ежедневно засевал на 5 га больше, чем было предусмотрено планом, поэтому сев был закончен на 2 дня раньше срока. Определите засеянную площадь.
8. Два каменщика сложили стену за 20 дней. За сколько дней выполнил бы эту работу каждый из них в отдельности, если известно, что первому пришлось бы работать на 9 дней больше, чем второму?
9. Теплоход загружается подъемными кранами. Сначала в течение 4 ч работали три крана одинаковой мощности, затем к ним присоединились еще два крана большей мощности, и через 3 ч после этого загрузка была закончена. Если бы все краны начали работать одновременно, то погрузка была бы закончена за 6 ч. За какое время выполнят погрузку один кран меньшей мощности и один кран большей мощности, работая вместе?
10. Вода из трех кранов заполнила резервуар за 12 минут, причем первый кран был открыт 4 минуты, и за это время было заполнено 40 % резервуара. За сколько минут заполнил бы резервуар каждый кран, если известно, что второй кран за 5 минут наливает столько воды, сколько третий кран за 6 минут?
Источник http://spacemath.xyz/proizvoditelnost/
Источник https://stroitelstvo-gid.ru/sovety/dva-ekskavatora-rabotaya-odnovremenno-mogut-vyryt-kotlovan-za-6-ch-40-min.html
Источник https://mathembs.blogspot.com/p/21.html